今回から3回にわたってF1に関する流体・空気力学について詳しく解説していきます。ちょっとした計算式なども加えてありますのでよりエアロに詳しくなれるのではと思います。また数学が苦手!という人でもわかるような説明を心がけますので、安心して読み進めてください。
数式なしで超簡単に説明している記事はこちら!
「F1で学ぶ流体・空気力学その1」では圧力とダウンフォースの発生原理を解説します。
圧力の重要性
まず初めに、F1の空気力学で重要視されている圧力について説明していきます。
F1マシンは空気から力を加えられることによって空気抵抗やダウンフォースを生み出しています。空気の力は圧力の差によって生まれるので、マシン周りの圧力を計算することによってマシンがどの方向からどのくらいの力を加えられるのかがわかります。
翼の例をみていきましょう。

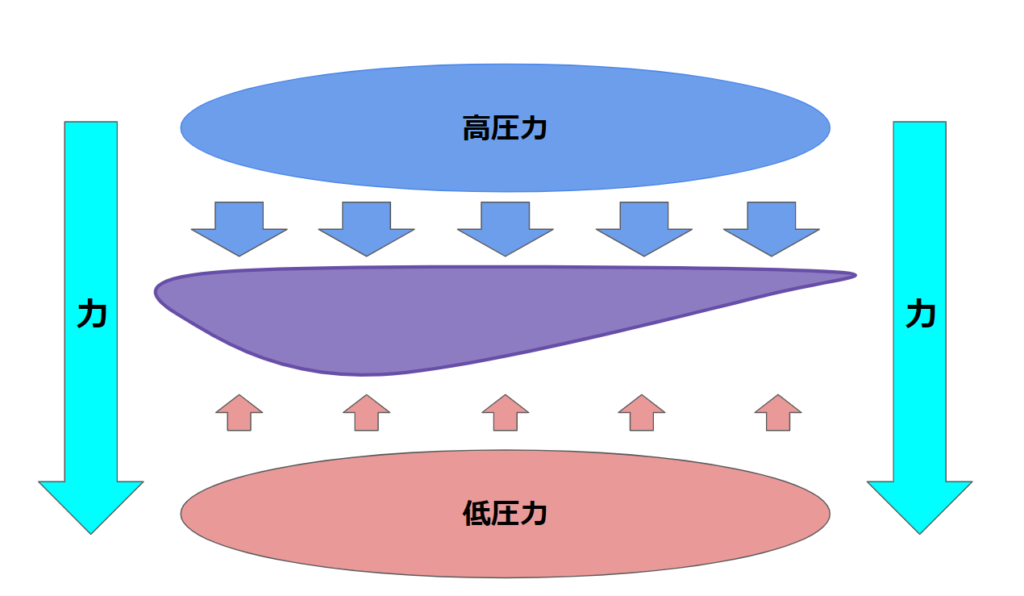
F1の翼ではダウンフォースを発生させていますが、これは翼の上面と下面での圧力に差があるためです。上面の圧力のほうが下面の圧力より大きいため、力は下向きに働きます。また一部の空気抵抗も同じ原理で起こります。
このようにダウンフォースと空気抵抗に直接かかわってくる圧力は特に調査が必要な要素となっているのです。
圧力の計算方法
走行中のF1マシンのような流体中の物体に加わる圧力の計算は二段階あります。まず初めに物質の置かれた環境のコンディションを調べ、それから物質近辺の圧力を調べていきます。
その1 大気環境のコンディションを調べる
F1を例に考えてみましょう。
F1マシンは水中や油の中ではなく、空気中を、それも大気中を走行していますね。ということは大気のコンディションによってマシンに加わる圧力が変化しそうなことは想像に容易いのではないでしょうか。ここで気体に関する方程式を見てみましょう。
\( P V = m R T \)
この式は気体の状態方程式といい、\( P \)が圧力、\( V \)が気体が占める体積、\( m \)が質量、\( R \)が気体定数、\( T \)が絶対温度を表します。
気体に関する変数として圧力、体積、分子数、温度があり、そのうちいずれか三つがわかればもう一つがわかります。また大気を調べるときは体積を考えることはできないので、単位体積あたりの質量、つまり密度にすることで計算が可能となります。
\( P = ρ R T \)
\( ρ \) : 密度 \( = \dfrac{m}{V} \)
状態方程式の使い方としてはレース日の気温や、大気圧から空気の密度を計算することができます。空気密度はダウンフォースに密接にかかわってくるのでとても重要なパラメータになります。
マシン周りの圧力を調べる
環境のパラメータがわかったところでマシン周りの圧力を調べてみましょう。
一般に流体の速度と圧力は密接にかかわっており、ベルヌーイの定理によって示されています。
\( \dfrac{1}{2} ρ v^2 + p = const. \)
\( ρ \) : 流体密度 \( v \) : 流体速度 \( p \) : 圧力 \( const. \) : 一定の意
この式は流体がもつエネルギーは常に一定ということを表しています。ちなみに圧力もエネルギーの形の一つととらえることができます。一番目の項は運動エネルギーを表しています。
つまり流体の運動エネルギーが増加すると圧力は減少し、運動エネルギーが減少すると圧力は増加します。運動エネルギーは速度の2乗に比例するので、速度が増加すると圧力は減少し、速度が減少すると圧力が増加します。
また密度は定数という扱いになるので、この関係式では直接圧力に影響があるわけではありません。しかし密度が高いということはトータルのエネルギー量が増加するので圧力も増加することになります。
さてここで疑問になるのはどのようにすると速度が変わるかですね。実は流体の流れる範囲を限定することで速度の調整が可能なのです。
ベンチュリ管をみてみましょう。

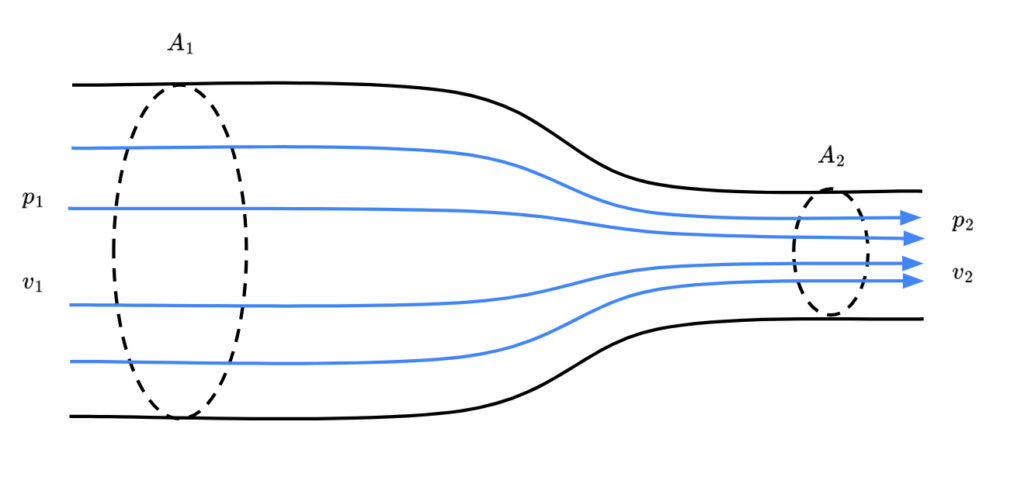
ベンチュリ管とは流路の一部の径が小さくなっている管です。
ここで重要なのは径の大きさが変化しても流量はどこでも一定ということです。あるとこまではある流量で途中から少ない流量になったら当然つまりが起きてしまいますね。ということは径が小さくなったら必然的に速度があがらないといけません。これは質量流量保存の法則としてこのように記述されます。
\( ρ_1 A_1 v_1 = ρ_2 A_2 v_2 \)
F1の速度領域では流体密度はほぼ一定とみなしてもいいので質量の代わりに体積をもちいた式でも問題ありません。よって
\( A_1 v_1 = A_2 v_2 \)
つまり流体の流路範囲を狭めると速度が増加し、逆に流路範囲を広げると速度は低下します。
この性質を用いてウィングは設計されています。
ウィングの形状
ベルヌーイの定理を踏まえた上でウィングの形状をみてみましょう。
F1のウィングは下側に膨らみをもっています。ここに流体を流してみるとウィングの下側の流速が速くなります。膨らみによってウィング入り口より流路範囲が狭まっていることが原因です。

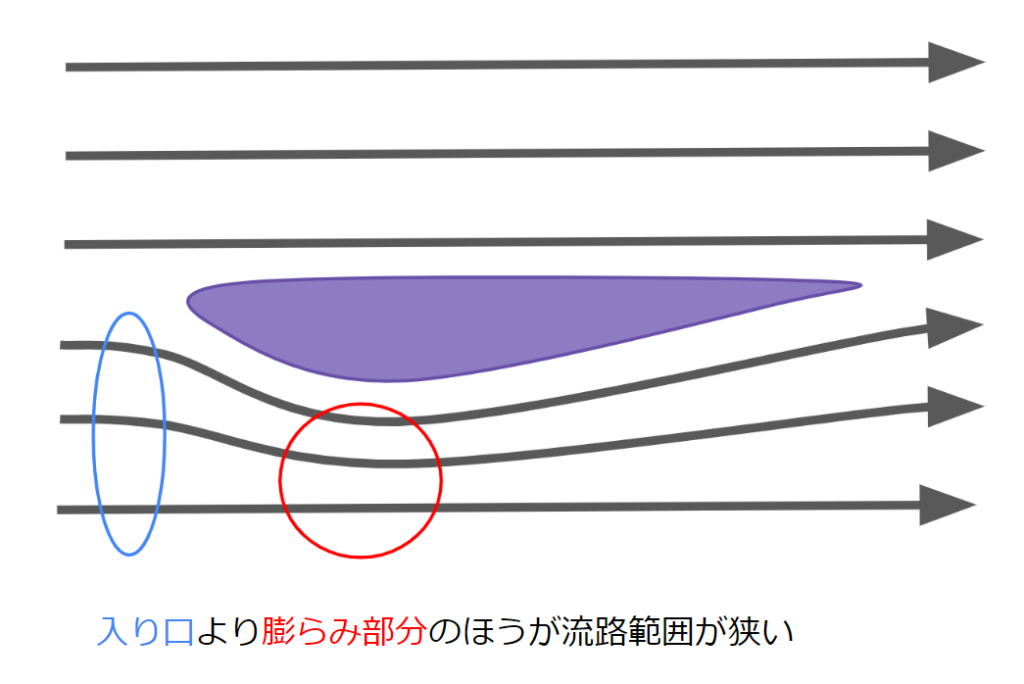
しかし上側は流路範囲に変化がないのでもともとの速度で流れています。
ベルヌーイの定理より、下側の流速が増加したことで圧力が下がり、上側と下側の圧力差により下向きの力が加わります。
ウィングの角度によるダウンフォースの発生
実は圧力差のほかにもう一つダウンフォースを生み出す方法があります。
ウィングは傾けることで空気の流れの向きを変えることができます。空気の流れの向きを変えるということは空気に対して力を加えていることになります。物体に対して力を加えると反作用を受けます。これを使って空気の流れを上向きに変えることでダウンフォースを受けることができます。

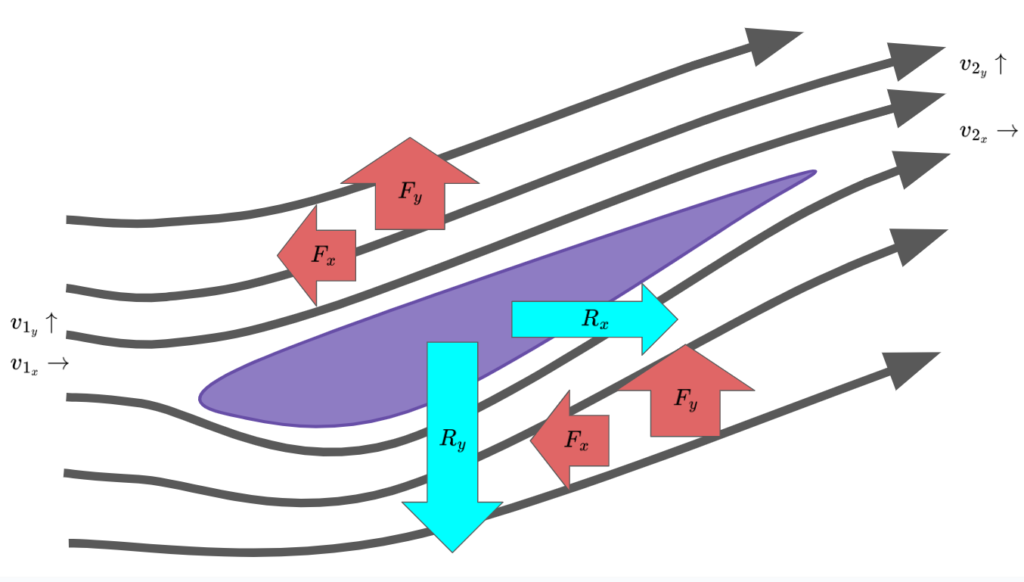
力の大きさは運動量保存の法則を使用できます。
\( F = ρ Q (v_2 – v_1) \)
\( F \) : 力ベクトル \( Q \) : 体積流量 \( v_2 \) : 出口での流速ベクトル \( v_1 \) : 入口での流速ベクトル
ベクトルになっているのはそれぞれ\( x \)成分と\( y \)成分が含まれているからです。力ベクトルの\( x \)成分は空気抵抗に、\( y \)成分はダウンフォースとなります。
角度を大きく変えることができればダウンフォースが大きくなるということですね。
まとめ
今回学んだことをポイントごとにまとめました。
- F1マシンは周りの空気の圧力差によって力を受ける
- 状態方程式を用いて大気のコンディション、得に空気密度を計算できる
- ベルヌーイの定理・流体質量保存の法則より、ウィングの形状は下側を膨らませるとダウンフォースを発生させる
- ウィングを傾けて空気を上にはね上げることで反作用が働きダウンフォースを発生させる。その大きさは運動量保存の法則より求められる。
今回ウィングの傾きによってダウンフォースを得られると解説しましたが、角度がきつすぎるとそれができない場合があります。次回ではそれがなぜできないのか、またそれを可能にする方法についても解説したいと思います。






コメント